Kernel PCA Made Fast: The Nyström Approximation

Why Kernel PCA?

Standard PCA finds linear patterns in your data. But what if your data has non-linear structure? Consider these two concentric circles:

set.seed(42)
# Create two concentric circles
n <- 200
theta <- runif(n, 0, 2*pi)
inner <- cbind(3*cos(theta), 3*sin(theta)) + rnorm(2*n, sd=0.1)
outer <- cbind(8*cos(theta), 8*sin(theta)) + rnorm(2*n, sd=0.1)
X_circles <- rbind(inner, outer)
colors <- c(rep("blue", n), rep("red", n))

par(mfrow = c(1, 2))
# Original data
plot(X_circles, col = colors, pch = 19, cex = 0.5,
     main = "Original Data", xlab = "X", ylab = "Y")

# Standard PCA fails
pca_result <- pca(X_circles, ncomp = 2)
plot(pca_result$s, col = colors, pch = 19, cex = 0.5,
     main = "Standard PCA", xlab = "PC1", ylab = "PC2")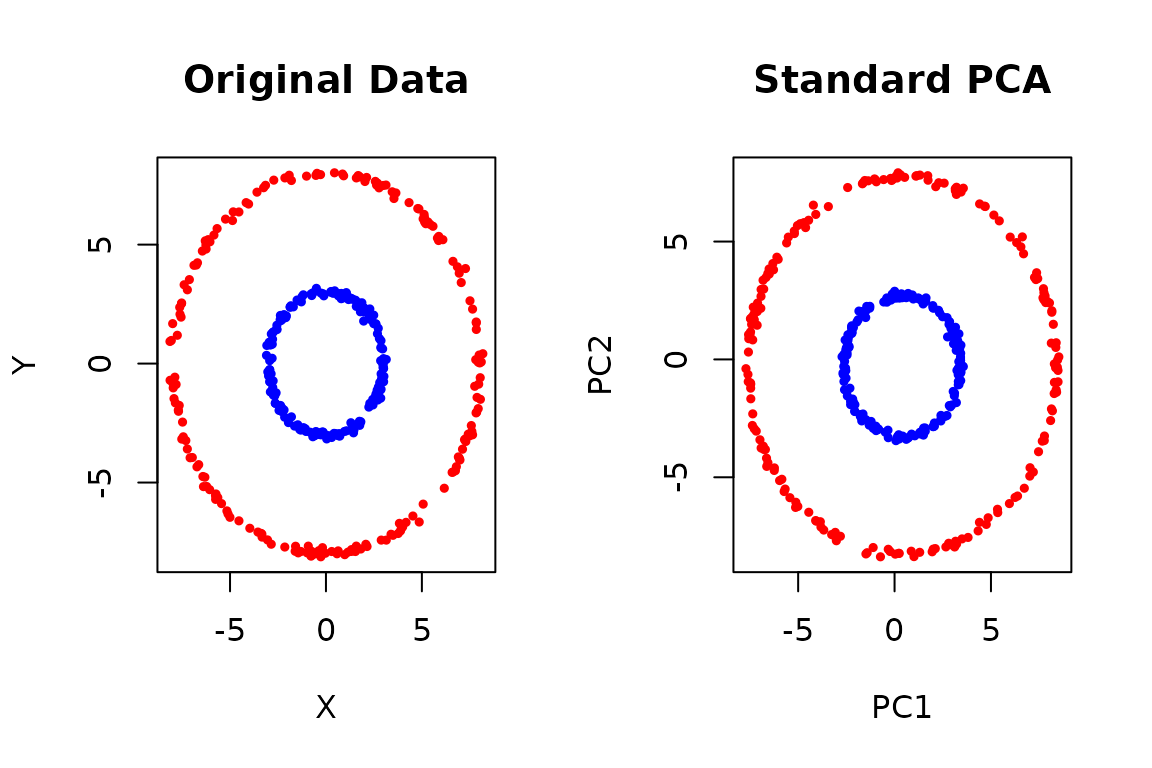

Standard PCA can’t separate these circles because they’re not linearly separable. Kernel PCA solves this by implicitly mapping the data to a higher-dimensional space where linear separation becomes possible.

The Challenge: Computational Cost

Kernel PCA requires computing a kernel matrix K where K[i,j] = k(x_i, x_j) for some kernel function k. For N samples: - Memory: O(N²) to store K - Time: O(N³) for eigendecomposition

This becomes prohibitive for large datasets (N > 10,000).

The Solution: Nyström Approximation

The Nyström method approximates the full kernel matrix using only a small subset of “landmark” points:

Select m << N landmark points
Compute kernel values only between:
- Landmarks vs landmarks (m × m matrix)
- All points vs landmarks (N × m matrix)
Use these to approximate the full eigendecomposition

This reduces complexity from O(N³) to O(Nm²), a huge speedup when m is small!

Quick Start Example

Let’s apply kernel PCA to our circles using the Nyström approximation:

# Define a simple RBF (Gaussian) kernel
rbf_kernel <- function(X, Y = NULL, sigma = 1) {
  if (is.null(Y)) Y <- X
  
  # Compute squared distances efficiently
  sumX2 <- rowSums(X^2)
  sumY2 <- rowSums(Y^2)
  sqdist <- outer(sumX2, sumY2, `+`) - 2 * tcrossprod(X, Y)
  sqdist[sqdist < 0] <- 0  # Fix numerical issues
  
  exp(-sqdist / (2*sigma^2))
}

# Apply Nyström approximation
ny_result <- nystrom_approx(
  X_circles,
  kernel_func = rbf_kernel,
  ncomp = 2,          # Number of components
  nlandmarks = 50     # Only 50 landmarks for 400 points!
)

# Plot the results
plot(ny_result$s, col = colors, pch = 19, cex = 0.5,
     main = "Kernel PCA via Nyström", 
     xlab = "Component 1", ylab = "Component 2")

Success! The Nyström approximation separated the circles using only 50 landmark points instead of all 400.

Using nystrom_approx()

The nystrom_approx() function returns a standard bi_projector object:

# Check what we got
print(ny_result)
#> A bi_projector object with the following properties:
#> 
#> Dimensions of the weights (v) matrix:
#>   Rows:  400  Columns:  2 
#> 
#> Dimensions of the scores (s) matrix:
#>   Rows:  400  Columns:  2 
#> 
#> Length of the standard deviations (sdev) vector:
#>   Length:  2 
#> 
#> Preprocessing information:
#> A finalized pre-processing pipeline:
#>  Step  1 : pass

# Project new data
new_points <- rbind(
  c(4, 0),   # Should be inner circle
  c(0, 8),   # Should be outer circle
  c(5.5, 5.5) # Between circles
)
new_scores <- project(ny_result, new_points)
print(new_scores)
#>               [,1]         [,2]
#> [1,] -9.720225e-02 5.752583e-06
#> [2,] -3.821218e-10 3.006193e-13
#> [3,] -2.294905e-09 3.194746e-13

Advanced Options

1. Automatic Kernel Parameter Selection

The kernel bandwidth (sigma) greatly affects results. Here’s a kernel with automatic parameter selection:

# RBF kernel with median heuristic for sigma
auto_rbf_kernel <- function(X, Y = NULL, sigma = NULL) {
  if (is.null(Y)) Y <- X
  
  if (is.null(sigma)) {
    # Use median distance heuristic on a sample
    n_sample <- min(nrow(X), 100)
    idx <- sample(nrow(X), n_sample)
    dists <- as.vector(dist(X[idx, ]))
    sigma <- median(dists[dists > 0]) / sqrt(2)
    message("Auto-selected sigma = ", round(sigma, 3))
  }
  
  sumX2 <- rowSums(X^2)
  sumY2 <- rowSums(Y^2)
  sqdist <- outer(sumX2, sumY2, `+`) - 2 * tcrossprod(X, Y)
  sqdist[sqdist < 0] <- 0
  
  exp(-sqdist / (2*sigma^2))
}

# Use it
ny_auto <- nystrom_approx(X_circles, kernel_func = auto_rbf_kernel,
                          ncomp = 2, nlandmarks = 50)
#> Auto-selected sigma = 5.927
#> Auto-selected sigma = 5.276

2. Double Nyström for Extra Speed

For very large datasets, “Double Nyström” applies the approximation twice:

# Create a larger dataset
set.seed(123)
n_large <- 2000
theta_large <- runif(n_large, 0, 2*pi)
radius_large <- sample(c(3, 8), n_large, replace = TRUE)
X_large <- cbind(radius_large*cos(theta_large), 
                 radius_large*sin(theta_large)) + rnorm(2*n_large, sd=0.1)

# Standard Nyström
system.time(
  ny_standard <- nystrom_approx(X_large, kernel_func = auto_rbf_kernel,
                                ncomp = 5, nlandmarks = 200, 
                                method = "standard")
)
#> Auto-selected sigma = 5.45
#> Auto-selected sigma = 5.381
#>    user  system elapsed 
#>   0.030   0.026   0.019

# Double Nyström (faster for same number of landmarks)
system.time(
  ny_double <- nystrom_approx(X_large, kernel_func = auto_rbf_kernel,
                              ncomp = 5, nlandmarks = 200,
                              method = "double", l = 50)
)
#> Auto-selected sigma = 4.916
#> Auto-selected sigma = 4.851
#> Auto-selected sigma = 5.4
#>    user  system elapsed 
#>   0.045   0.100   0.042

3. Preprocessing Integration

You can combine kernel PCA with preprocessing:

# Center and scale before kernel PCA
ny_preprocessed <- nystrom_approx(
  X_circles,
  kernel_func = rbf_kernel,
  ncomp = 2,
  nlandmarks = 50,
  preproc = colscale(center(), type = "z")  # Preprocessing pipeline: center then scale
)

Choosing Parameters

Number of Landmarks (m)

Dataset Size	Suggested Landmarks	Notes
< 1,000	50-200	Can use larger fraction
1,000-10,000	200-500	Good accuracy/speed balance
> 10,000	500-2,000	Consider Double Nyström

Method Selection

Standard Nyström: Use when m < 2,000 and highest accuracy is needed
Double Nyström: Use for very large datasets or when m > 2,000

Common Kernels

# Linear kernel (equivalent to standard PCA)
linear_kernel <- function(X, Y = NULL) {
  if (is.null(Y)) tcrossprod(X) else tcrossprod(X, Y)
}

# Polynomial kernel
poly_kernel <- function(X, Y = NULL, degree = 3, coef = 1) {
  if (is.null(Y)) Y <- X
  (tcrossprod(X, Y) + coef)^degree
}

# Sigmoid kernel
sigmoid_kernel <- function(X, Y = NULL, alpha = 1, coef = 0) {
  if (is.null(Y)) Y <- X
  tanh(alpha * tcrossprod(X, Y) + coef)
}

When to Use Nyström Approximation

✓ Use when: - Your dataset has > 5,000 samples - You need non-linear dimensionality reduction - Full kernel PCA is too slow/memory-intensive - Approximate solutions are acceptable

✗ Don’t use when: - You have < 1,000 samples (use full kernel PCA) - You need exact results - Linear PCA suffices for your problem

Technical Details

Click for mathematical details

The Nyström approximation uses the fact that a positive semi-definite kernel matrix K can be approximated as:

$K \approx K_{nm} K_{mm}^{-1} K_{mn}$

where: - $K_{mm}$ is the m × m kernel matrix between landmarks - $K_{nm}$ is the N × m kernel matrix between all points and landmarks

The eigendecomposition of this approximation can be computed efficiently: 1. Compute eigendecomposition of $K_{mm} = U_m \Lambda_m U_m^T$ 2. Approximate eigenvectors of K as: $U \approx K_{nm} U_m \Lambda_m^{-1/2}$

Double Nyström applies this approximation recursively within the landmark computation, reducing complexity from O(Nm² + m³) to O(Nml + l³) where l << m.