Shared-Basis HRF Matching (SBHM): Efficient Voxel-Specific HRF Estimation

Introduction

Shared-Basis HRF Matching (SBHM) provides an efficient middle ground between global HRF selection (one HRF for all voxels) and fully unconstrained voxel-wise HRF estimation. SBHM learns a low-rank shared time basis from a library of candidate HRFs, then matches each voxel to its best-fitting library member in a reduced coefficient space.

The Problem: Voxel-Specific HRFs at Scale

Real fMRI data shows substantial HRF variability across brain regions and individuals. A single canonical HRF (like SPM’s double-gamma) often provides a poor fit to the data. However, estimating completely unconstrained voxel-wise HRFs using FIR bases or multi-basis models is:

Computationally expensive: Requires fitting many parameters per voxel
Data hungry: Needs many trials for stable estimates
High variance: Individual voxel estimates can be noisy without regularization

The SBHM Solution

SBHM addresses these challenges by:

Learning a shared basis from a library of physiologically plausible HRFs via SVD
Fitting voxels in the low-dimensional basis space (typically r=4-8 dimensions)
Matching each voxel to its closest library member using cosine similarity
Projecting trial-wise coefficients onto matched coordinates for interpretable amplitudes

This approach provides: - Efficiency: Fit only r parameters per voxel (vs. K×trials for FIR) - Stability: Constrain estimates to a learned manifold of plausible HRFs - Interpretability: Each voxel maps to a specific library HRF with known parameters

When to Use SBHM

Use SBHM when: - You expect voxel-specific HRF shapes but want them library-constrained - Your library is large (50-200+ candidate HRFs) covering physiological variability - You want computational efficiency with interpretable per-voxel HRF assignments - You need to compare HRF parameters across voxels or conditions

Use global HRF selection when: - A single shared HRF is sufficient for your analysis - Maximum computational efficiency is critical - Your ROI is anatomically homogeneous

Use unconstrained voxel-wise HRF when: - You need to discover completely novel HRF shapes - You have many trials and can afford the variance - You want data-driven HRF discovery without parametric constraints

Use multi-basis or FIR when: - You need to capture timing/shape variability within single trials - Your experimental design varies trial-to-trial (e.g., parametric modulation)

library(fmrihrf)
library(fmrilss)

# Derived convenience defaults for examples
n_voxels_default <- if (fast_mode) 20 else 50
n_trials_default <- if (fast_mode) 6 else 10
ranks_default    <- if (fast_mode) 2:6 else 2:10

SBHM Workflow Overview

The SBHM pipeline consists of four main steps, coordinated by the lss_sbhm() function:

1. sbhm_build()    → Learn shared basis B from HRF library via SVD
                     Returns: B (time basis), S (singular values), A (library coordinates)

2. sbhm_prepass()  → Fit aggregate model in basis space per voxel
                     Returns: beta_bar (r×V coefficients)

3. sbhm_match()    → Match voxels to library via cosine similarity
                     Returns: matched_idx, margin, alpha_hat

4. LSS + Project   → Run OASIS with K=r, project to scalar amplitudes
                     Returns: trial-wise amplitudes (ntrials×V)

We’ll walk through each step with examples, then show the end-to-end workflow.

Step 1: Building the Shared Basis

The first step is to create a library of candidate HRFs spanning physiological variability, then learn a low-rank basis via SVD.

Creating an HRF Library

# Define a parameter grid for gamma HRFs
# Shape controls peak time, rate controls width
shapes <- if (fast_mode) seq(6, 10, by = 2) else seq(5, 11, by = 1.5)
rates  <- if (fast_mode) seq(0.8, 1.2, by = 0.2) else seq(0.7, 1.3, by = 0.15)
param_grid <- expand.grid(shape = shapes, rate = rates)

cat("Library size:", nrow(param_grid), "HRFs\n")
#> Library size: 9 HRFs

# Function to create gamma HRF with given parameters
gamma_fun <- function(shape, rate) {
  # Important: close over parameters so evaluation uses (shape, rate)
  f <- function(t) fmrihrf::hrf_gamma(t, shape = shape, rate = rate)
  fmrihrf::as_hrf(f, name = sprintf("gamma(s=%.2f,r=%.2f)", shape, rate), span = 32)
}

# Set up time grid
sframe <- sampling_frame(blocklens = n_time, TR = TR)

# Build SBHM with rank r=6
sbhm <- sbhm_build(
  library_spec = list(
    fun = gamma_fun,
    pgrid = param_grid,
    span = 32,           # HRF duration in seconds
    precision = 0.1,     # Time resolution for evaluation (0.1s steps)
    method = "conv"      # Convolution method (vs. "interp")
  ),
  r = 6,                 # Target rank (number of basis functions)
  sframe = sframe,
  baseline = c(0, 0.5),  # Remove mean in first 0.5s (before response)
  normalize = TRUE,      # L2 normalize library columns before SVD
  shifts = NULL,         # Optional: time shifts to augment library (experimental)
  ref = "mean"           # Reference HRF: "mean" (library average) or "spmg1" (SPM canonical)
)

cat("\nSBHM basis dimensions:\n")
#> 
#> SBHM basis dimensions:
cat("  B (time basis):", dim(sbhm$B), "\n")
#>   B (time basis): 160 6
cat("  S (singular values):", length(sbhm$S), "\n")
#>   S (singular values): 6
cat("  A (library coords):", dim(sbhm$A), "\n")
#>   A (library coords): 6 9

# Estimate total library variance via a higher-rank SVD for a more meaningful percent
max_r <- min(12, n_time, nrow(sbhm$A))
sbhm_full <- sbhm_build(
  library_spec = list(fun = gamma_fun, pgrid = param_grid, span = 32),
  r = max_r,
  sframe = sframe,
  baseline = c(0, 0.5),
  normalize = TRUE
)
cat("  Variance explained by r=6:",
    round(100 * sum(sbhm$S^2) / sum(sbhm_full$S^2), 1), "%\n")
#>   Variance explained by r=6: 100 %

Visualizing the Learned Basis

# Plot the learned time basis functions
par(mfrow = c(2, 3), mar = c(3, 3, 2, 1))
for (i in 1:ncol(sbhm$B)) {
  plot(sbhm$tgrid, sbhm$B[, i], type = "l", col = "navy", lwd = 2,
       main = paste0("Basis ", i, " (σ=", round(sbhm$S[i], 2), ")"),
       xlab = "Time (s)", ylab = "Amplitude")
  abline(h = 0, col = "gray", lty = 2)
  grid()
}

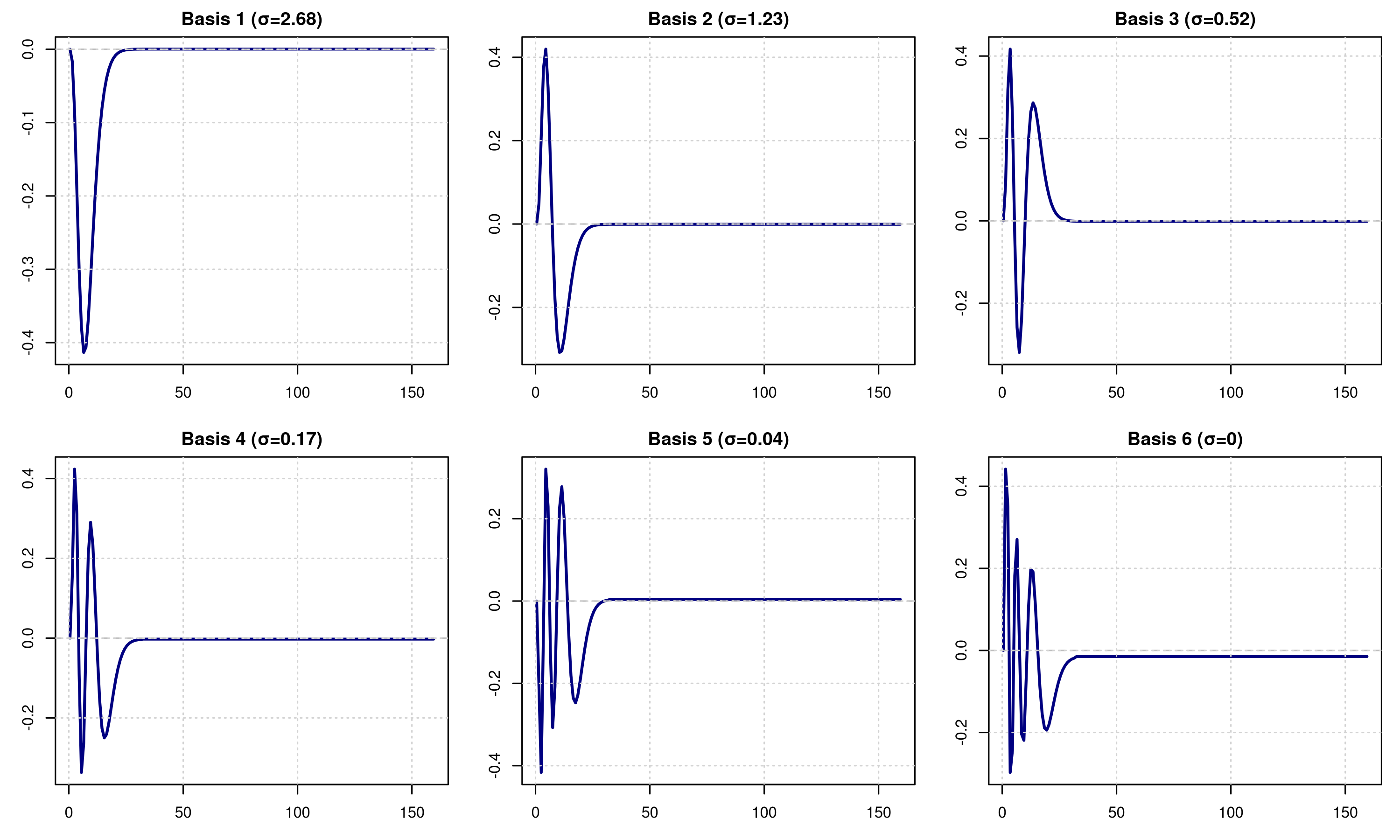
Understanding the Basis

The basis functions capture the principal modes of variation in the HRF library:

Basis 1 typically captures the main hemodynamic response shape
Basis 2-3 capture timing variations (earlier vs. later peaks)
Basis 4-6 capture width and undershoot variations

The singular values (S) indicate the importance of each basis function. A rapid drop-off suggests redundancy in the library.

Choosing the Rank (r)

# Build SBHM with different ranks to see variance explained
ranks <- ranks_default
var_explained <- numeric(length(ranks))

for (i in seq_along(ranks)) {
  sbhm_test <- sbhm_build(
    library_spec = list(fun = gamma_fun, pgrid = param_grid, span = 32),
    r = ranks[i],
    sframe = sframe,
    normalize = TRUE
  )
  var_explained[i] <- sum(sbhm_test$S^2)
}

plot(ranks, var_explained / max(var_explained) * 100,
     type = "b", pch = 19, col = "navy", lwd = 2,
     xlab = "Rank (r)", ylab = "Variance Explained (%)",
     main = "Choosing SBHM Rank")
abline(h = 95, col = "red", lty = 2)
grid()
text(8, 97, "95% threshold", col = "red", pos = 3)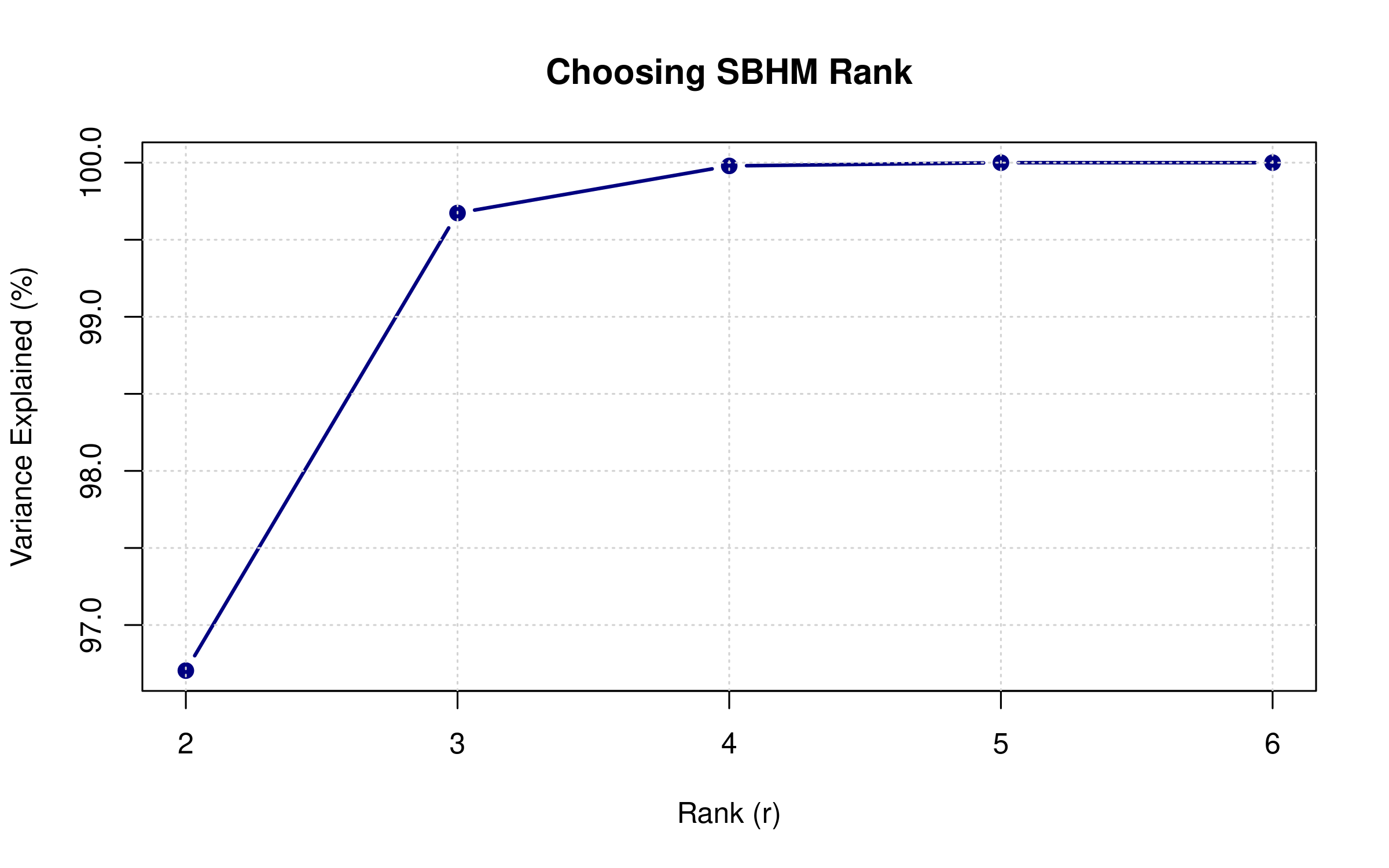

Library Coverage Intuition

# Visualize a subset of library shapes reconstructed from B and A
H_hat <- sbhm$B %*% sbhm$A  # T×K (rank-r reconstruction)
K <- ncol(H_hat)
sel <- unique(round(seq(1, K, length.out = min(K, 12))))
matplot(sbhm$tgrid, H_hat[, sel, drop = FALSE], type = "l", lty = 1,
        col = colorRampPalette(c("#6baed6", "#08519c"))(length(sel)), lwd = 1.5,
        xlab = "Time (s)", ylab = "Amplitude",
        main = "Sample of Library HRFs (rank-r reconstruction)")
abline(h = 0, col = "gray80", lty = 2)
grid()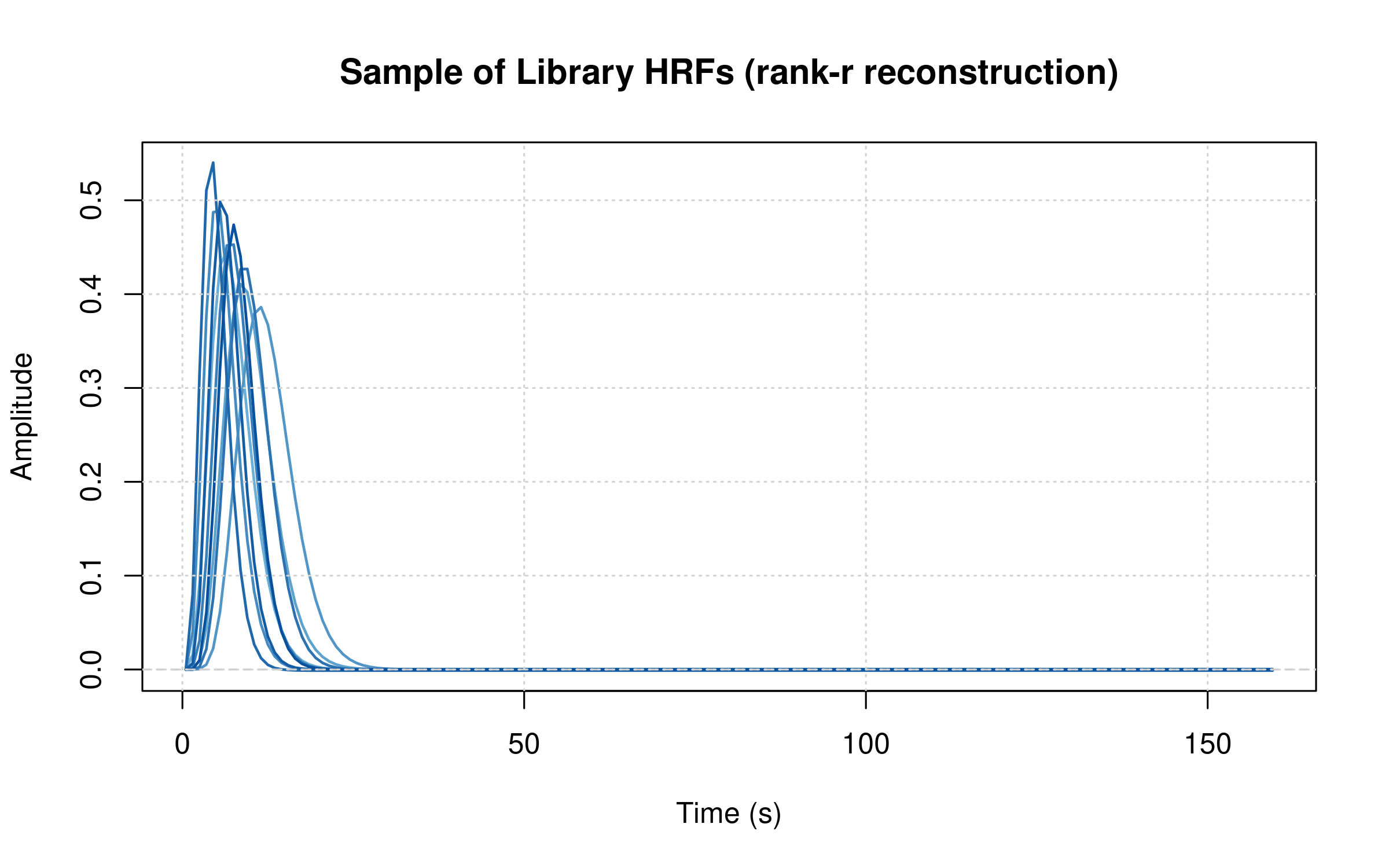

Guidelines for choosing r: - Start with r=6 for gamma libraries, r=8-10 for more complex libraries - Aim for 90-95% variance explained - Balance: larger r = better library coverage, but more parameters to fit - Typical range: r=4 (simple) to r=12 (complex)

Understanding the Reference HRF

The ref parameter in sbhm_build() determines the reference HRF used for: 1. Shrinkage target in matching (pulls noisy estimates towards reference) 2. Orientation alignment via orient_ref (flips coefficients to match reference polarity)

# Option 1: Mean of library (default, data-driven)
sbhm_mean <- sbhm_build(..., ref = "mean")
# Reference = average of all library HRFs

# Option 2: SPM canonical HRF (theory-driven)
sbhm_spm <- sbhm_build(..., ref = "spmg1")
# Reference = SPM's double-gamma canonical HRF

When to use each: - “mean” (recommended): Let your library define the typical response - “spmg1”: For compatibility with SPM analyses or when library is exploratory

The reference is stored in sbhm$ref$alpha_ref (r-dimensional coordinates).

Step 2: Generating Synthetic Data with Known HRF Variation

To demonstrate SBHM’s ability to recover voxel-specific HRFs, we’ll create synthetic data where different voxels have different HRF shapes from our library.

# Experimental design
n_voxels <- n_voxels_default
n_trials <- n_trials_default
# Place trial onsets safely within the acquisition window so HRFs are observed
safe_end <- max(sbhm$tgrid) - 30  # leave HRF span margin (~30s)
onsets <- seq(20, safe_end, length.out = n_trials)

# Assign each voxel a random HRF from the library
set.seed(456)
true_hrf_idx <- sample(ncol(sbhm$A), n_voxels, replace = TRUE)

# Generate trial-wise design using SBHM basis
design_spec <- list(
  sframe = sframe,
  cond = list(onsets = onsets, duration = 0, span = 30)
)

hrf_B <- sbhm_hrf(sbhm$B, sbhm$tgrid, sbhm$span)
rr <- regressor(
  onsets = onsets,
  hrf = hrf_B,
  duration = 0,
  span = 30,
  summate = FALSE
)
# Build per-trial regressors explicitly (one K-column block per trial)
regressors_by_trial <- vector("list", n_trials)
for (t in 1:n_trials) {
  rr_t <- regressor(onsets = onsets[t], hrf = hrf_B, duration = 0, span = 30, summate = FALSE)
  X_t  <- evaluate(rr_t, grid = sbhm$tgrid, precision = 0.1, method = "conv")
  regressors_by_trial[[t]] <- X_t  # T×K
}

# Create signal: each voxel uses its assigned HRF's coordinates
Y <- matrix(rnorm(n_time * n_voxels, sd = 0.5), n_time, n_voxels)
true_amplitudes <- matrix(rnorm(n_trials * n_voxels, mean = 2, sd = 0.5),
                          n_trials, n_voxels)

for (v in 1:n_voxels) {
  # Get the true HRF coordinates for this voxel
  alpha_true <- sbhm$A[, true_hrf_idx[v]]

  # Add signal: X_trials * alpha_true gives the per-trial regressors
  # Each trial's amplitude scales this regressor
  for (t in 1:n_trials) {
    regressor_t <- regressors_by_trial[[t]] %*% alpha_true
    Y[, v] <- Y[, v] + true_amplitudes[t, v] * regressor_t
  }
}

cat("Data generated:\n")
#> Data generated:
cat("  Y dimensions:", dim(Y), "\n")
#>   Y dimensions: 160 20
cat("  True HRF assignments:", length(unique(true_hrf_idx)), "unique HRFs\n")
#>   True HRF assignments: 9 unique HRFs

Step 3: Running the Complete SBHM Pipeline

Now we’ll use lss_sbhm() to recover the voxel-specific HRFs and trial amplitudes.

Prewhitening for Autocorrelated Noise

If your fMRI data has temporally correlated noise (common with short TR < 2s), prewhitening improves parameter estimates:

# Example with AR(1) prewhitening via fmriAR
res_prewhiten <- lss_sbhm(
  Y = Y, sbhm = sbhm, design_spec = design_spec,
  prewhiten = list(method = "ar", p = 1L, pooling = "global", exact_first = "ar1"),
  ...
)

When to use prewhitening: - TR < 2s (high temporal resolution) - Visual inspection shows autocorrelated residuals - Improved model fit is critical (e.g., single-subject studies)

Note: Prewhitening is applied during the prepass stage. It cannot be combined with data_fac (PCA factorization).

Basic SBHM Run

# Run end-to-end SBHM (no prewhitening for this synthetic example)
res_sbhm <- lss_sbhm(
  Y = Y,
  sbhm = sbhm,
  design_spec = design_spec,
  Nuisance = NULL,
  prewhiten = NULL,  # Set to list(method="ar", p=1L, exact_first="ar1") for short TR
  prepass = list(
    ridge = list(mode = "fractional", lambda = 0.01)  # Small ridge for stability
  ),
  match = list(
    shrink = list(tau = 0, ref = sbhm$ref$alpha_ref),
    topK = 1,
    whiten = TRUE,      # Whiten by singular values before matching
    orient_ref = TRUE   # Flip coefficient sign if anti-correlated with reference
                        # Ensures consistent polarity across voxels
  ),
  oasis = list(
    ridge_mode = "fractional",  # Scale ridge by mean eigenvalue (recommended)
    ridge_x = 0.01,   # Regularize design matrix (X'X + ridge_x*I) for stability
    ridge_b = 0.01    # Shrink coefficients towards zero for variance reduction
  ),
  return = "both"  # Return both amplitudes and coefficients
)

cat("SBHM results:\n")
#> SBHM results:
cat("  Amplitude dimensions:", dim(res_sbhm$amplitude), "\n")
#>   Amplitude dimensions: 6 20
cat("  Coefficients dimensions:", dim(res_sbhm$coeffs_r), "\n")
#>   Coefficients dimensions: 6 6 20
cat("  Matched HRF indices:", length(res_sbhm$matched_idx), "\n")
#>   Matched HRF indices: 20

Step 4: Evaluating HRF Recovery

Let’s assess how well SBHM recovered the true HRF assignments.

# Check matching accuracy
matched_idx <- res_sbhm$matched_idx
accuracy <- mean(matched_idx == true_hrf_idx)

cat("HRF Matching Accuracy:", round(100 * accuracy, 1), "%\n")
#> HRF Matching Accuracy: 15 %
cat("Confused voxels:", sum(matched_idx != true_hrf_idx), "/", n_voxels, "\n\n")
#> Confused voxels: 17 / 20

# Analyze matching confidence via margin (top1 - top2 score)
cat("Matching confidence (margin):\n")
#> Matching confidence (margin):
cat("  Mean:", round(mean(res_sbhm$margin), 3), "\n")
#>   Mean: 0.21
cat("  Median:", round(median(res_sbhm$margin), 3), "\n")
#>   Median: 0.2
cat("  Range:", round(range(res_sbhm$margin), 3), "\n")
#>   Range: 0.002 0.317

# Low margin indicates ambiguity
low_confidence <- which(res_sbhm$margin < median(res_sbhm$margin))
cat("  Low-confidence voxels (<median):", length(low_confidence), "\n")
#>   Low-confidence voxels (<median): 10

Visualizing Matching Confidence

hist(res_sbhm$margin, breaks = 20, col = "skyblue", border = "white",
     main = "Distribution of Matching Confidence (Margin)",
     xlab = "Margin (Top1 - Top2 cosine score)",
     ylab = "Number of Voxels")
abline(v = median(res_sbhm$margin), col = "red", lwd = 2, lty = 2)
text(median(res_sbhm$margin), par("usr")[4] * 0.9,
     "Median", pos = 4, col = "red")
grid()

Interpreting margin: - High margin (>0.1): Clear winner, high confidence - Medium margin (0.05-0.1): Moderate confidence, top 2 candidates similar - Low margin (<0.05): Ambiguous, consider averaging top-K candidates

Note on top-K: lss_sbhm() uses hard assignment (top-1) internally. For soft assignment, call sbhm_prepass() and sbhm_match(topK = K) directly to obtain weights and topK_idx, then combine candidate coordinates manually before projecting via sbhm_project().

Comparing Recovered vs. True Amplitudes

# Correlation between estimated and true amplitudes
cor_amp <- cor(as.vector(res_sbhm$amplitude), as.vector(true_amplitudes))

plot(as.vector(true_amplitudes), as.vector(res_sbhm$amplitude),
     pch = 19, col = adjustcolor("navy", alpha.f = 0.3),
     xlab = "True Amplitude", ylab = "SBHM Estimated Amplitude",
     main = paste0("Amplitude Recovery (r = ", round(cor_amp, 3), ")"))
abline(0, 1, col = "red", lwd = 2, lty = 2)
grid()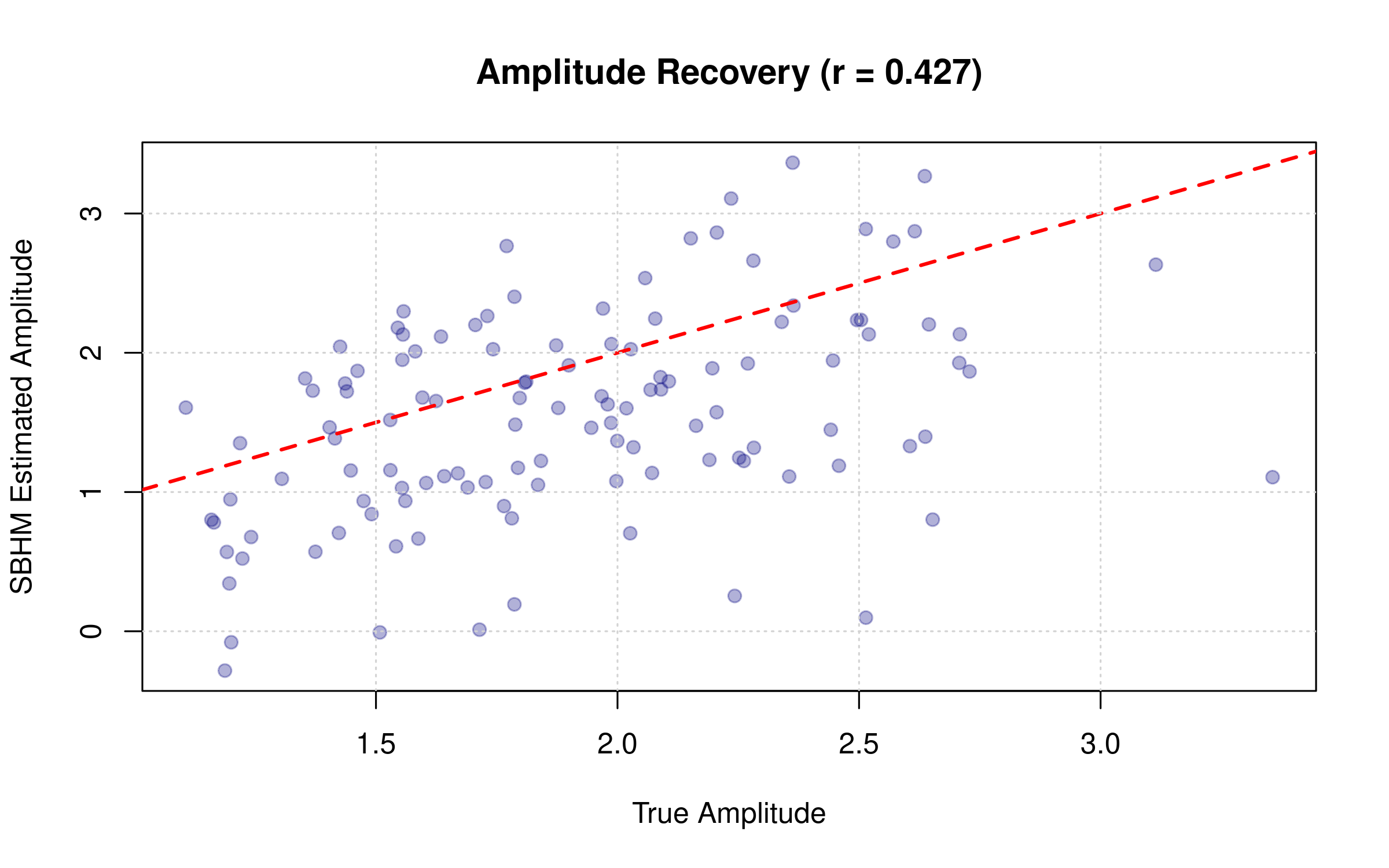

Library Manifold and Matches

# PCA of library coordinates (columns of A), overlay matched HRFs
A_t <- t(sbhm$A)  # K×r
pca <- prcomp(A_t, center = TRUE, scale. = TRUE)
pc <- pca$x[, 1:2, drop = FALSE]
plot(pc, pch = 16, col = "gray70",
     xlab = "PC1", ylab = "PC2",
     main = "Library Coordinate Space (PCA)")

# Highlight true and matched HRFs
points(pc[unique(true_hrf_idx), , drop = FALSE], pch = 1, col = "#2c7fb8", lwd = 2)
points(pc[unique(res_sbhm$matched_idx), , drop = FALSE], pch = 4, col = "#d95f02", lwd = 2)
legend("topright", bty = "n",
       legend = c("Library", "True HRFs", "Matched HRFs"),
        pch = c(16, 1, 4), col = c("gray60", "#2c7fb8", "#d95f02"))
grid()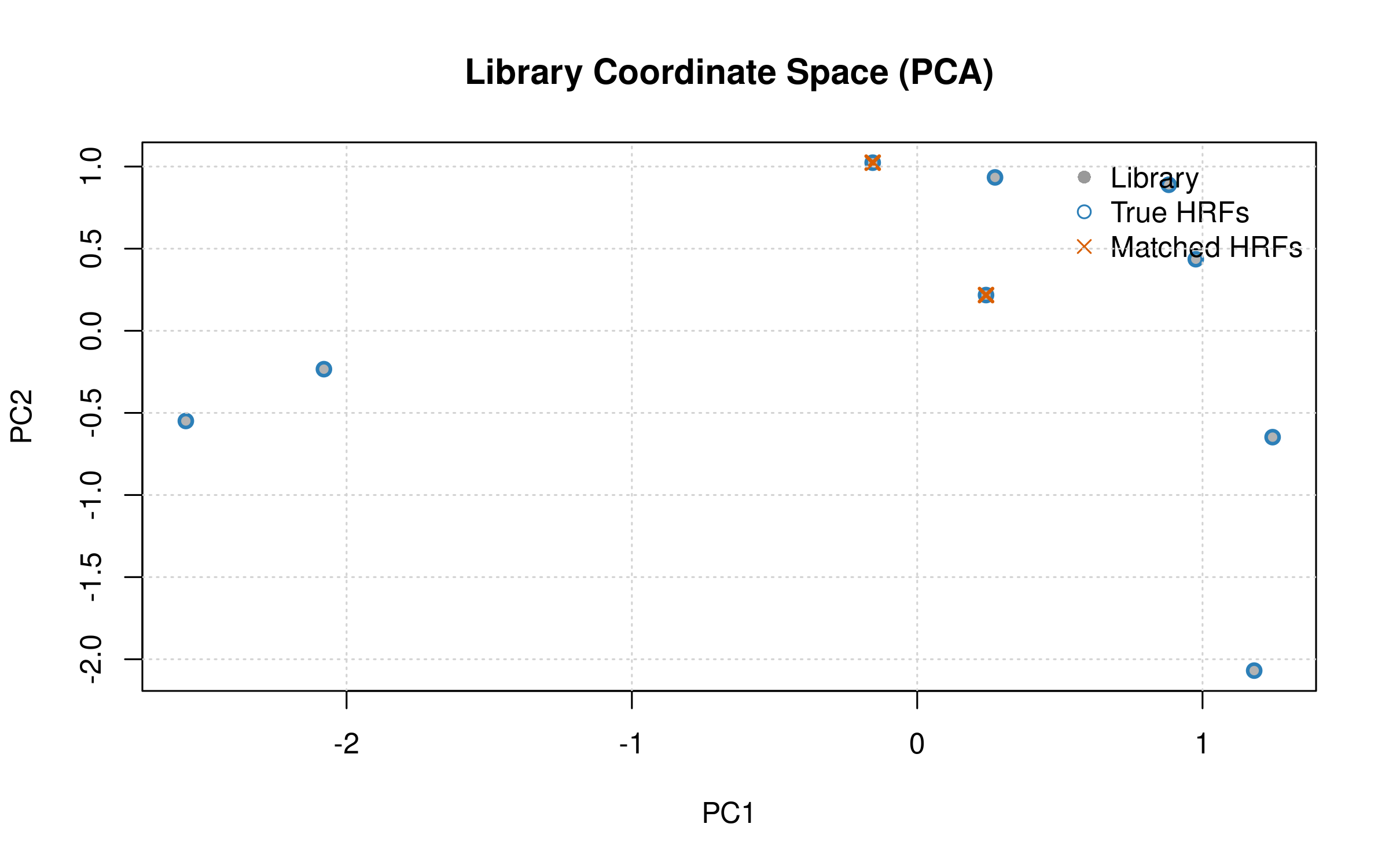

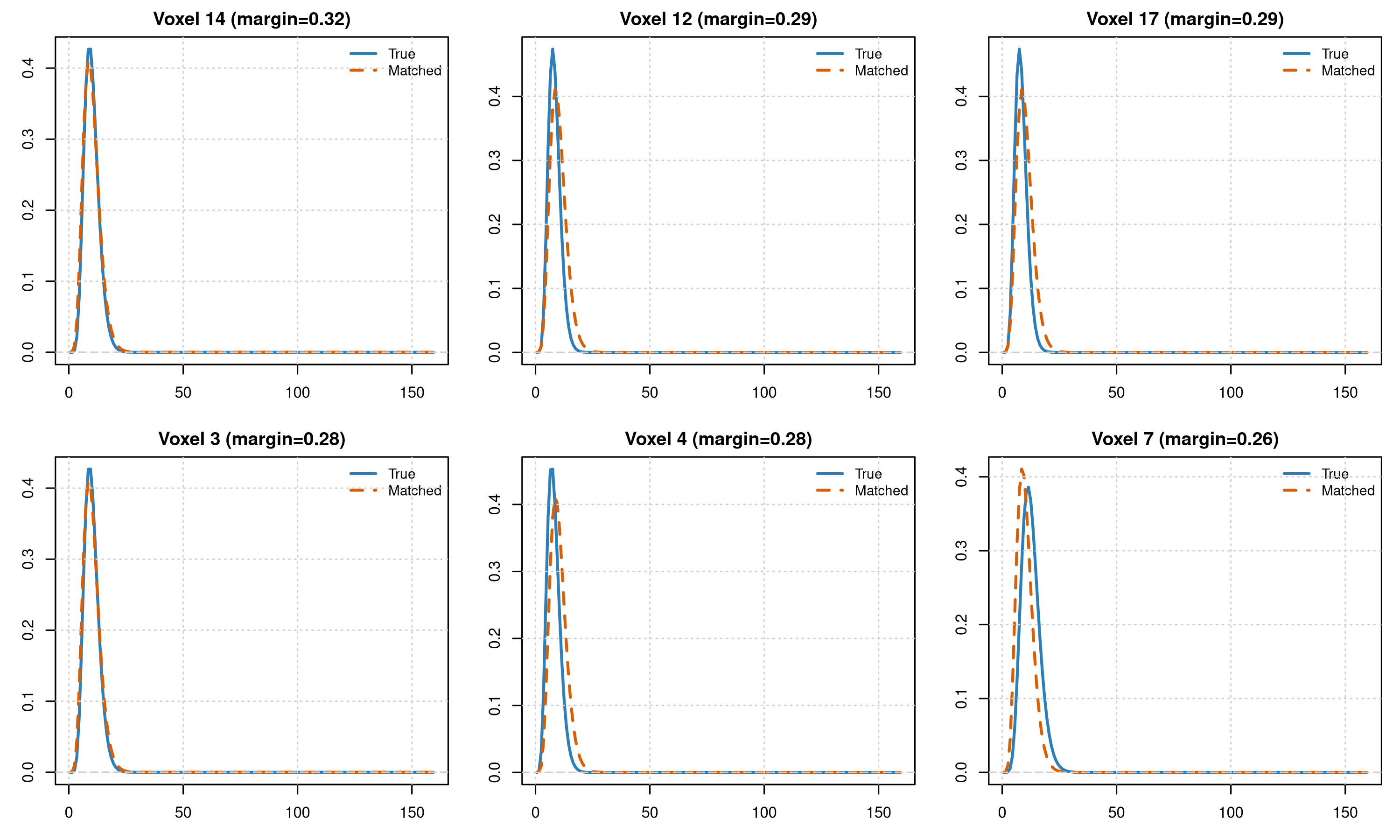
Matched vs. True HRF Shapes

# Compare matched HRF shapes to true HRFs for a few voxels
H_hat <- sbhm$B %*% sbhm$A
vox_show <- head(order(-res_sbhm$margin), n = min(6, n_voxels))  # confident voxels
par(mfrow = c(2, 3), mar = c(3, 3, 2, 1))
for (v in vox_show) {
  h_true <- H_hat[, true_hrf_idx[v]]
  h_match <- H_hat[, res_sbhm$matched_idx[v]]
  rng <- range(c(h_true, h_match))
  plot(sbhm$tgrid, h_true, type = "l", col = "#2c7fb8", lwd = 2,
       main = paste0("Voxel ", v, " (margin=", round(res_sbhm$margin[v], 2), ")"),
       xlab = "Time (s)", ylab = "HRF", ylim = rng)
  lines(sbhm$tgrid, h_match, col = "#d95f02", lwd = 2, lty = 2)
  abline(h = 0, col = "gray80", lty = 2)
  legend("topright", bty = "n", cex = 0.9,
         legend = c("True", "Matched"), lty = c(1, 2), lwd = 2,
         col = c("#2c7fb8", "#d95f02"))
  grid()
}

Understanding SBHM Parameters

Parameter Quick Reference

This table summarizes all SBHM parameters with recommended starting values:

Parameter	Default	Recommended Range	When to Adjust
r (rank)	—	6 (simple) to 12 (complex)	Aim for 90-95% variance explained
topK (matching)	1	1 (hard) to 5 (soft)	Use 3-5 for ambiguous cases
ridge.lambda (prepass)	0.01	0.005 to 0.05	Add 0.01-0.05 for noisy data
ridge.mode	“fractional”	“fractional” or “absolute”	Fractional scales by design energy
shrink.tau (matching)	0	0 to 0.2	Increase for low SNR (0.1-0.2)
whiten	TRUE	TRUE (recommended)	Set FALSE to weight by singular values
orient_ref	TRUE	TRUE (recommended)	Ensures consistent coefficient polarity
ridge_x (OASIS design)	0	0.01 to 0.05	Increase if design ill-conditioned
ridge_b (OASIS coeffs)	0	0.01 to 0.05	Increase for variance reduction
prewhiten	NULL	NULL or list(method=“ar”, p=1L)	Use for TR < 2s or autocorrelated noise
data_fac	NULL	NULL or PCA factorization	Use for V > 50,000 voxels

Minimal call (uses all defaults except required arguments):

res <- lss_sbhm(Y = Y, sbhm = sbhm, design_spec = design_spec)
# Uses: small fractional ridge (0.01), topK=1, whiten=TRUE, orient_ref=TRUE, no prewhitening

Prepass Ridge Regularization

The prepass fits aggregate coefficients per voxel. Ridge helps with: - Collinear basis functions (if library has redundancy) - Low SNR data - Preventing extreme coefficients

# Example: varying ridge strength
prepass = list(
  ridge = list(
    mode = "fractional",    # Scale by design energy
    lambda = 0.01,          # 1% of mean eigenvalue
    alpha_ref = sbhm$ref$alpha_ref  # Shrink towards reference
  )
)

Guidelines: - Start with lambda = 0.01 (small fractional ridge) - Increase to 0.02–0.05 if unstable or low SNR - Use mode = "fractional" for automatic scaling by design energy

Matching Shrinkage

Shrinkage pulls noisy voxel estimates towards a reference before matching, reducing the influence of noise on HRF assignment.

match = list(
  shrink = list(
    tau = 0.1,              # Shrinkage strength (0 = none, 1 = full shrinkage to ref)
    ref = sbhm$ref$alpha_ref,  # Shrinkage target (library mean by default)
    snr = NULL              # Optional: per-voxel SNR for adaptive shrinkage
  )
)

When to use: - Low SNR data: tau = 0.1-0.2 (stronger shrinkage) - High SNR data: tau = 0 (no shrinkage) - Adaptive shrinkage: provide per-voxel SNR estimates

Adaptive Shrinkage with SNR

For heterogeneous SNR across voxels, adaptive shrinkage adjusts tau per voxel:

# Compute per-voxel SNR from prepass (higher SNR = less shrinkage)
# Simple proxy: ratio of aggregate fit variance to residual variance
prepass_result <- sbhm_prepass(Y, sbhm, design_spec)
# Proxy SNR: variance explained by aggregate fit vs. residual variance
fit <- prepass_result$A_agg %*% prepass_result$beta_bar  # in residualized space
signal_var <- apply(fit, 2, stats::var)
total_var  <- apply(Y,   2, stats::var)
residual_var <- pmax(total_var - signal_var, .Machine$double.eps)
snr_voxel <- pmax(signal_var, .Machine$double.eps) / residual_var

match = list(
  shrink = list(
    tau = NULL,  # NULL triggers adaptive mode
    ref = sbhm$ref$alpha_ref,
    snr = snr_voxel  # Higher SNR voxels get less shrinkage
  )
)

Adaptive formula: For voxel v, effective tau = base_tau / (1 + snr[v]), where base_tau is calibrated internally.

Whitening

Whitening divides coefficients by singular values before matching, equalizing the importance of all basis directions.

match = list(
  whiten = TRUE  # Recommended: divides by S before L2 normalization
)

Effect: Without whitening, the first basis (largest S) dominates matching. With whitening, all r dimensions contribute equally to the cosine score.

Advanced Use Cases

Working with Top-K Matches

Instead of hard assignment to the single best HRF, you can get the top-K candidates with weights.

# Demonstrate top-K matching directly via sbhm_prepass + sbhm_match
pre_small <- sbhm_prepass(
  Y = Y[, 1:10],  # Subset for speed
  sbhm = sbhm,
  design_spec = design_spec
)
m_top3 <- sbhm_match(
  beta_bar = pre_small$beta_bar,
  S = sbhm$S,
  A = sbhm$A,
  topK = 3,
  whiten = TRUE
)

cat("Top-3 matching (subset):\n")
#> Top-3 matching (subset):
cat("  Top indices dims:", dim(m_top3$topK_idx), "\n")
#>   Top indices dims: 3 10
cat("  Weights dims:", dim(m_top3$weights), "\n")
#>   Weights dims: 3 10

# Examine one voxel's top-3 matches
v <- 1
cat("\nVoxel", v, "top-3:\n")
#> 
#> Voxel 1 top-3:
for (k in 1:3) {
  cat("  Rank", k, ": HRF", m_top3$topK_idx[k, v],
      "(weight =", round(m_top3$weights[k, v], 3), ")\n")
}
#>   Rank 1 : HRF 2 (weight = 0.373 )
#>   Rank 2 : HRF 5 (weight = 0.321 )
#>   Rank 3 : HRF 8 (weight = 0.307 )

Soft Assignment End-to-End

Hard assignment uses only the top-1 HRF per voxel. Soft assignment blends the top-K candidates using their softmax weights, then projects trial-wise coefficients onto this blended coordinate to produce amplitudes. This can reduce variance for ambiguous voxels (small margin) at the cost of some bias.

Conceptually: - Prepass: estimate per-voxel basis coefficients beta_bar. - Match: compute cosine scores in whitened, L2-normalized space; convert top-K scores into softmax weights (temperature = 1) per voxel. - Blend: compute weighted average of the unwhitened library coordinates A[:, idx] using those weights to form alpha_soft (r×V). - LSS: obtain trial-wise r-dimensional coefficients (K=r) with OASIS. - Project: amplitudes = inner product of trial-wise coefficients with alpha_soft.

# 1) Prepass on all voxels
pre_all <- sbhm_prepass(Y = Y, sbhm = sbhm, design_spec = design_spec)

# 2) Top-K matching with softmax weights
topK <- 3
m_soft <- sbhm_match(
  beta_bar = pre_all$beta_bar,
  S = sbhm$S,
  A = sbhm$A,
  topK = topK,
  whiten = TRUE,
  orient_ref = TRUE
)

# 3) Build blended coordinates alpha_soft (r×V)
V <- ncol(Y)
r <- nrow(pre_all$beta_bar)
alpha_soft <- matrix(0, nrow = r, ncol = V)
for (v in seq_len(V)) {
  idx <- m_soft$topK_idx[, v]
  w   <- m_soft$weights[, v]
  # Weighted combination in unwhitened coordinate space
  alpha_soft[, v] <- as.numeric(sbhm$A[, idx, drop = FALSE] %*% w)
}

# 4) Trial-wise coefficients with OASIS (K=r)
hrf_B <- sbhm_hrf(sbhm$B, sbhm$tgrid, sbhm$span)
spec  <- design_spec; spec$cond$hrf <- hrf_B
BetaMat <- lss(
  Y = Y, X = NULL, Z = NULL, Nuisance = NULL,
  method = "oasis",
  oasis = list(design_spec = spec, K = r),
  prewhiten = NULL
)
stopifnot(nrow(BetaMat) %% r == 0)
ntrials <- nrow(BetaMat) / r
beta_rt <- array(BetaMat, dim = c(r, ntrials, V))

# 5) Soft-assignment amplitudes
amps_soft <- sbhm_project(beta_rt, alpha_soft)

cat("Soft-assignment amplitudes dims:", dim(amps_soft), "\n")
#> Soft-assignment amplitudes dims: 6 20

# Optional: compare against hard-assignment amplitudes from lss_sbhm()
res_hard <- lss_sbhm(Y, sbhm, design_spec, return = "amplitude",
                     prepass = list(ridge = list(mode = "fractional", lambda = 0.01)))

cor_soft_hard <- cor(as.vector(amps_soft), as.vector(res_hard$amplitude))
cat("Correlation (soft vs hard amplitudes):", round(cor_soft_hard, 3), "\n")
#> Correlation (soft vs hard amplitudes): 0.912

# Focus on ambiguous voxels (low margin) where soft can help
ambig <- which(res_hard$margin < median(res_hard$margin))
if (length(ambig) >= 3) {
  cat("Ambiguous voxels (n):", length(ambig), "\n")
}
#> Ambiguous voxels (n): 10

Built-in Soft Assignment (Convenience)

For convenience, lss_sbhm() can also perform soft blending internally to avoid manual steps. Set match = list(topK = 3, soft_blend = TRUE) and optionally a blend_margin to only blend ambiguous voxels.

res_soft <- lss_sbhm(
  Y = Y,
  sbhm = sbhm,
  design_spec = design_spec,
  prepass = list(ridge = list(mode = "fractional", lambda = 0.01)),
  match = list(topK = 3, soft_blend = TRUE, blend_margin = median(res_hard$margin)),
  return = "amplitude"
)

cor_built <- cor(as.vector(res_soft$amplitude), as.vector(res_hard$amplitude))
cat("Correlation (built-in soft vs hard):", round(cor_built, 3), "\n")
#> Correlation (built-in soft vs hard): 0.96

Best practices for soft assignment: - Use when margin is small (ambiguous matches). Consider blending only for voxels with margin < threshold and keep hard assignment otherwise. - The weights are a softmax over cosine scores (temperature = 1). To sharpen or smooth, you can post-process scores with a custom temperature before exponentiation. - Blending trades interpretability (single HRF per voxel) for stability. Report both the matched index and whether soft blending was applied.

Returning Coefficients for Custom Analysis

# Get trial-wise coefficients in basis space
res_coeffs <- lss_sbhm(
  Y = Y[, 1:5],
  sbhm = sbhm,
  design_spec = design_spec,
  return = "coefficients"  # Don't project to amplitudes
)

cat("Coefficient array dimensions:", dim(res_coeffs$coeffs_r), "\n")
#> Coefficient array dimensions: 6 6 5
cat("  [1] = basis dimension (r)\n")
#>   [1] = basis dimension (r)
cat("  [2] = number of trials\n")
#>   [2] = number of trials
cat("  [3] = number of voxels\n")
#>   [3] = number of voxels

# You can now do custom projections or analyses in coefficient space

Performance Considerations

Computational Cost

SBHM cost scales as: - Build: O(T²·K) for library SVD (one-time) - Prepass: O(T²·r + T·r·V) per voxel aggregate fit - Match: O(r·K·V) for cosine scores - LSS: O(T·r·N·V) for N trials, r-dimensional design

Compared to alternatives: - vs. Global grid search: ~2-3x slower (r fits vs. 1 fit per candidate) - vs. Voxel-wise FIR: ~10-50x faster (r parameters vs. K·N parameters) - vs. Unconstrained per-voxel: ~5-20x faster

Memory Usage

Peak memory scales with: - Data: T·V (input fMRI data) - Design: T·r·N (trial-wise basis design) - Coefficients: r·N·V (trial-wise basis coefficients)

For T=300, V=100k, r=6, N=100: ~2GB for coefficients.

Optimization Tips

1. Data Factorization for Whole-Brain Analysis

For very large datasets (V > 50,000 voxels), use PCA factorization to reduce memory and computation:

# Compute PCA decomposition: Y ≈ scores × loadings'
pca <- prcomp(Y, center = TRUE, rank. = 100)  # Keep q=100 components
Y_pca <- list(
  scores = pca$x,       # T×q (time × components)
  loadings = pca$rotation  # q×V (components × voxels)
)

# Run SBHM on factored data (fits q "meta-voxels" instead of V voxels)
res_sbhm <- lss_sbhm(
  Y = Y_pca$scores,  # Pass scores as Y
  sbhm = sbhm,
  design_spec = design_spec,
  prepass = list(
    data_fac = list(
      scores = Y_pca$scores,    # T×q
      loadings = Y_pca$loadings # q×V (transposed internally)
    )
  )
)

Trade-offs: - Speedup: ~V/q times faster prepass (e.g., 100x for V=100k, q=100) - Accuracy: Loses information in discarded components (minor for q=100-200) - Limitation: Cannot use with prewhiten (incompatible operations)

When to use: V > 50,000 and memory is limited, or when prepass is the bottleneck.

2. Process in ROI Chunks

# For targeted analyses, process specific brain regions
roi_mask <- my_roi_definition  # Logical vector
Y_roi <- Y[, roi_mask]
res_roi <- lss_sbhm(Y_roi, sbhm, design_spec)

3. Reduce Library Size if Matching is Slow

# SBHM matching is O(r·K·V), so K matters for large V
# Option: Cluster library in parameter space and use centroids
param_clusters <- kmeans(param_grid, centers = 50)
pgrid_reduced <- param_grid[unique(param_clusters$cluster), ]

4. Library Augmentation with Time Shifts (Experimental)

The shifts parameter augments the library by time-shifting each HRF:

# Add shifted versions of each HRF (e.g., ±1s shifts)
sbhm_shifted <- sbhm_build(
  library_spec = list(fun = gamma_fun, pgrid = param_grid, span = 32),
  r = 8,  # May need higher rank for shifted library
  sframe = sframe,
  shifts = c(-1, 0, 1),  # Create 3 versions: 1s early, on-time, 1s late
  normalize = TRUE
)
# Library size increases by length(shifts) factor (K → K×3)

Use cases: - Uncertain event timing (e.g., subject-paced tasks) - Modeling temporal jitter in HRF onset - Exploratory analyses

Caution: Increases library size (computational cost) and risk of overfitting.

Comparison with Other Approaches

SBHM vs. Global HRF Selection

Aspect	SBHM	Global Selection
Per-voxel HRFs	✓ Yes	✗ Single shared HRF
Computation	Moderate	Fast
Interpretability	High (library params)	High (single model)
Flexibility	Library-constrained	Fully constrained
Best for	Heterogeneous regions	Homogeneous ROIs

SBHM vs. Unconstrained Voxel-Wise

Aspect	SBHM	Unconstrained
Parameters/voxel	r (4-8)	K·N (50-500+)
Stability	High (regularized)	Lower (needs many trials)
Interpretability	High (library mapping)	Lower (arbitrary shapes)
Flexibility	Library-constrained	Fully flexible
Best for	Known HRF variability	Novel HRF discovery

Troubleshooting

Low Matching Accuracy

Symptoms: Many voxels assigned incorrect HRFs, low correlation with ground truth

Possible causes: 1. Library doesn’t cover the true HRF shapes 2. Low SNR making coefficient estimates noisy 3. Insufficient trials for stable prepass fit

Solutions: - Expand library to cover more parameter space - Increase shrinkage: tau = 0.1-0.2 - Add ridge regularization to prepass - Increase number of trials in experiment

High Variance in Amplitudes

Symptoms: Amplitudes have high trial-to-trial variability, low test-retest reliability

Possible causes: 1. Matched HRF is wrong (using wrong projection) 2. Low SNR in data 3. Insufficient ridge in OASIS step

Solutions: - Check matching confidence via margin - Increase OASIS ridge: ridge_x = 0.05-0.1 - Use top-K averaging instead of hard assignment

Slow Computation

Symptoms: SBHM takes much longer than expected

Possible causes: 1. Very large library (K > 200) 2. High rank (r > 12) with many voxels 3. Dense event designs with many trials

Solutions: - Reduce library size via clustering in parameter space - Lower rank: start with r=6 - Process ROIs separately instead of whole-brain

References

Mumford et al. (2012). “Deconvolving BOLD activation in event-related designs for multivoxel pattern classification analyses.” NeuroImage.
Lindquist et al. (2009). “Modeling the hemodynamic response function in fMRI.” NeuroImage.
Friston et al. (1998). “Event-related fMRI: Characterizing differential responses.” NeuroImage.

Summary

SBHM provides an efficient, interpretable approach to voxel-specific HRF estimation by:

Learning a shared basis from a physiologically plausible library
Matching voxels to library members via cosine similarity in coefficient space
Estimating trial-wise activations with per-voxel HRF shapes

Key advantages: - Computational efficiency (fit r parameters per voxel, not K·N) - Built-in regularization via library constraint - Interpretable HRF assignments with confidence scores - Integrates seamlessly with OASIS LSS framework

Next steps: - See ?sbhm_build for library construction details - See ?lss_sbhm for full parameter documentation - See the “Voxel-wise HRF” vignette for unconstrained alternatives - See the “OASIS Method” vignette for related approaches

fmrilss Development Team

2025-10-31